Resources: Secondary Maths
- [[Topics/Algebra|Algebra]]
- [[Topics/Algebra|Algebra]]
- [[Topics/Area|Area]]
- [[Topics/Perimeter|Perimeter]]
- [[Topics/Polygons|Polygons]]
- [[Topics/Area|Area]]
- [[Topics/Assessment|Assessment]]
- [[Topics/Consecutive Sums|Consecutive Sums]]
- [[Topics/Decimals|Decimals]]
- [[Topics/Graph transformations|Graph transformations]]
- [[Topics/Handling Data|Handling Data]]
- [[Topics/Investigation|Investigation]]
- [[Topics/Mean mode median|Mean mode median]]
- [[Topics/Prisms|Prisms]]
- [[Topics/Probability|Probability]]
- [[Topics/Rearranging formulae|Rearranging formulae]]
- [[Topics/Sequences|Sequences]]
- [[Topics/Shape|Shape]]
- [[Topics/Simultaneous Equations|Simultaneous Equations]]
- [[Topics/Standard Index Form|Standard Index Form]]
- [[Topics/Statistics|Statistics]]
- [[Topics/Symmetry|Symmetry]]
- [[Topics/Using images|Using images]]
Relevant resources
| Algebra | What's Possible? | |

|
Many numbers can be expressed as the difference of two perfect squares. What do you notice about the numbers you CANNOT make? This lesson idea is about exploring and noticing structure(ta).
The collection of NRICH activities are designed to develop students capacity to work as a mathematician. Exploring, questioning, working systematically, visualising, conjecturing, explaining, generalising, justifying, proving are all at the heart of mathematical thinking. This particular resource has been adapted from an original NRICH resource. NRICH promotes the learning of mathematics through problem solving. NRICH provides engaging problems, linked to the curriculum, with support for teachers in the classroom. Working on these problems will introduce students to key mathematical process skills. They offer students an opportunity to learn by exploring, noticing structure and discussing their insights, which in turn can lead to conjecturing, explaining, generalising, convincing and proof. The Teachers’ Notes provided focus on the pedagogical implications of teaching a curriculum that aims to provoke mathematical thinking. They assume that teachers will aim to do for students only what they cannot yet do for themselves. As a teacher, consider how this particular lesson idea can provoke mathematical thinking. How can you support students' exploration? How can you support conjecturing, explaining, generalising, convincing and proof?. | |
| Area | Circles, frustums and cylinders revision | |

|
Measure the volumes of objects This resource offer students the opportunity to engage in active learning(ta) - measuring and calculating using large size cylinders and frustums. This lesson brings great opportunity for small group "dialogic teaching(ta)". Open-ended and closed questioning(ta) of students can be used to draw on their existing knowledge and extend their understanding. The teacher provides a practical commentary below.
| |
| Assessment | Changing KS3 Questions for Engaging Assessment | |

|
A large set of questions grouped by topic, paper, and national curriculum level Test questions are often seen as uninteresting and useful only to assess pupils summatively. This resource however allows questioning(ta) to be used to support pupils’ revision, creativity and higher order(ta) problem-solving in class. The tasks could be conducted via whole class(ta) discussion(ta) or assessment(ta), perhaps using mini-whiteboards(tool), or in small group work(ta) situations.
| |
| Consecutive Sums | Using Prime and Square Numbers - How Old Am I? | |

|
Last year I was square, but this year I am in my prime. How old am I? This short activity offers opportunity for pupils to engage in mathematical thinking(ta) and higher order(ta) problem solving/reasoning(ta). They should be able to make links between different areas of mathematics and explore their ideas in whole class(ta) discussion(ta) and questioning(ta).
| |
| Handling Data | Olympic Records | |

|
Can you deduce which Olympic athletics events are represented by the graphs? This lesson idea is about reasoning, justifying, convincing and proof(ta).
The collection of NRICH activities are designed to develop students capacity to work as a mathematician. Exploring, questioning, working systematically, visualising, conjecturing, explaining, generalising, justifying, proving are all at the heart of mathematical thinking. This particular resource has been adapted from an original NRICH resource. NRICH promotes the learning of mathematics through problem solving. NRICH provides engaging problems, linked to the curriculum, with support for teachers in the classroom. Working on these problems will introduce students to key mathematical process skills. They offer students an opportunity to learn by exploring, noticing structure and discussing their insights, which in turn can lead to conjecturing, explaining, generalising, convincing and proof. The Teachers’ Notes provided focus on the pedagogical implications of teaching a curriculum that aims to provoke mathematical thinking. They assume that teachers will aim to do for students only what they cannot yet do for themselves. As a teacher, consider how this particular lesson idea can provoke mathematical thinking. How can you support students' exploration? How can you support conjecturing, explaining, generalising, convincing and proof?. | |
| Investigation | Consecutive Sums | |

|
Can all numbers be made in this way? For example 9=2+3+4, 11=5+6, 12=3+4+5, 20=2+3+4+5+6 By definition, a problem is something that you do not immediately know how to solve, so learning how to solve something unfamiliar is not straightforward. Tackling an extended problem is difficult.
This lesson gives pupils an opportunity to engage in mathematical thinking(ta) and develop their higher order(ta) thinking skills on a problem that is accessible but which has interest. For example, the problem is presented in diagrammatic and numerical ways. The plan suggests several visualisation(ta) methods to present the same underlying task. It should be useful for teachers to compare these different presentations and either to select the one that they feel will be most useful for their pupils or explore ways for the pupils to see the links between the different methods. The assessment(ta) ideas, using other pupils' solutions from the NRICH website are widely applicable to other problems too. | |
| Polygons | Exploring properties of rectangles: Perimeter and area. | |

|
Do two rectangles that have the same area also have the same perimeter? A problem to inspire higher order(ta) questioning(ta) especially in whole class(ta) dialogic teaching(ta) encouraging pupils to engage in mathematical thinking(ta) and language(ta). You could use Geogebra(tool) in this investigation, as an example of same-task group work(ta).
| |
| Probability | Playing with Probability - Efron's Dice | |

|
I have some dice that are coloured green, yellow, red and purple... Efron's dice provide a discussion(ta) topic for joint reasoning(ta) - whole class(ta) or in group work(ta). Pupils can explore aspects of mathematical thinking(ta) particularly with relation to probability.
| |
| Shape | Getting Your Formulae in Shape | |

|
Solving a card sort for perimeter, volume and area formulae This resource provides an opportunity for some revision of shape formulae - perimeter, area, and volume. It encourages pupils to engage in effectivereasoning(ta), and group talk(ta), and could be used as an effective assessment(ta) tool. The task could be differentiated(ta), or extended for a whole class by cutting the 'formulae' lines off the bottom of each hexagon, and asking students to match these to the shapes, prior to matching the shapes to the formulae type.
| |
| Simultaneous Equations | Love Food, Hate Waste - Simultaneous Equations | |

|
Using real world data to explore simultaneous equations Using a source that was not intended by its creators as a mathematical resource, pupils are introduced to informal ways of solving simultaneous equations.
The lesson starts with an intriguing ‘hook’, pupils are able to use reasoning(ta) skills to find an answer to the problem and can then, later, formalise this in an algebraic context, using their informal work to support the transition to mathematical thinking(ta). whole class(ta) work supports this inquiry(ta) into the data provided. Using a resource not targeted at mathematics specifically encourages pupils to think about maths outside of the classroom. | |
| Standard Index Form | An Introduction to the Standard Index Form | |
Working out the rules according to which a calculator displays large numbers The Standard Index Form is a key idea for mathematicians and scientists. The notion that we choose to write numbers in this way requires some explanation. So in this activity, pupils take part in an investigation(ta) on how standard index form works. This is a higher order(ta) problem solving context where students are encouraged to engage in mathematical thinking(ta). They may be involved in whole class(ta) or small group work(ta) discussion(ta), so they have a good opportunity to practice using mathematical language(ta) and questioning(ta).
This means that students do not need to be able to explain their ideas in full: they can use the calculator's feedback to discover whether their ideas are correct or not. This is also an exciting way for pupils to realise an initial idea that fits the data may need to be extended when new data arises. This resource therefore aims to develop investigative skills, as well as introduce pupils to standard index form in a memorable way. The pupils can later use their knowledge of indices in discussion(ta) and group talk(ta) as they explain what is happening. | ||
| Statistics | Cubic Equations and Their Roots | |
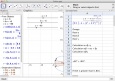
|
To interactiviley explore and understand complex mathematics with GeoGebra This lesson features a ‘real life’ example for students to explore using visualisation(ta) via GeoGebra. The focus on ‘real life’ increases student motivation.
The activity engages pupils in group talk(ta), mathematical thinking(ta) and vocabulary(ta). This open ended(ta) task encourages higher order(ta) thinking, and encourages whole class(ta) discussion(ta)/questioning(ta) and inquiry(ta) projects. | |
| Using images | Organising images for a narrative | |

|
Write an essay without words The lesson encourages students to think about how to portray their knowledge through narrative(ta) - which may engage some students who would usually be less interested. The lesson encourages students to think about how to capture valuable information and ensure that key elements are highlighted while not 'overloading' the viewer with data. The lesson can be tailored to any age group - for younger pupils the task could be to take before and after photos and label them. More advanced pupils might explore time-lapse photography. Pupils should be encouraged to think about how this relates to the scientific method(ta) The task is interactive and could be conducted as a group work(ta) activity or as an element of an inquiry-based learning project. It could also lend itself to whole class(ta) dialogue(ta) and the use of ICT(i) including 'clicker' response systems for assessment(ta) and questioning(ta).
| |
