Resources
- [[Topics/Algebra|Algebra]]
- [[Topics/Algebra|Algebra]]
- [[Topics/Area|Area]]
- [[Topics/Perimeter|Perimeter]]
- [[Topics/Polygons|Polygons]]
- [[Topics/Area|Area]]
- [[Topics/Assessment|Assessment]]
- [[Topics/Astronomy|Astronomy]]
- [[Topics/Geology|Geology]]
- [[Topics/Solar system|Solar system]]
- [[Topics/History|History]]
- [[Topics/Astronomy|Astronomy]]
- [[Topics/Biodiversity|Biodiversity]]
- [[Topics/E-safety|E-safety]]
- [[Topics/Blogs|Blogs]]
- [[Topics/E-skills|E-skills]]
- [[Topics/Curriculum development|Curriculum development]]
- [[Topics/Curriculum planning|Curriculum planning]]
- [[Topics/ICT|ICT]]
- [[Topics/Ethics|Ethics]]
- [[Topics/Cloning|Cloning]]
- [[Topics/Genetics|Genetics]]
- [[Topics/Consecutive Sums|Consecutive Sums]]
- [[Topics/Progression|Progression]]
- [[Topics/Curriculum development|Curriculum development]]
- [[Topics/Learning objectives|Learning objectives]]
- [[Topics/Literacy|Literacy]]
- [[Topics/Decimals|Decimals]]
- [[Topics/Digital Art|Digital Art]]
- [[Topics/Discussion|Discussion]]
- [[Topics/ICT|ICT]]
- [[Topics/Video|Video]]
- [[Topics/QR codes|QR codes]]
- [[Topics/Populations|Populations]]
- [[Topics/Ecology|Ecology]]
- [[Topics/Fertility treatments|Fertility treatments]]
- [[Topics/Human reproduction|Human reproduction]]
- [[Topics/Force|Force]]
- [[Topics/Genetics|Genetics]]
- [[Topics/Graph|Graph]]
- [[Topics/Graph transformations|Graph transformations]]
- [[Topics/Handling Data|Handling Data]]
- [[Topics/ICT|ICT]]
- [[Topics/Investigation|Investigation]]
- [[Topics/Living things|Living things]]
- [[Topics/Using images|Using images]]
- [[Topics/Materials|Materials]]
- [[Topics/Mean mode median|Mean mode median]]
- [[Topics/Measuring|Measuring]]
- [[Topics/Study skills|Study skills]]
- [[Topics/Patterns|Patterns]]
- [[Topics/Prisms|Prisms]]
- [[Topics/Probability|Probability]]
- [[Topics/Questioning|Questioning]]
- [[Topics/Scientific literacy|Scientific literacy]]
- [[Topics/Science citizenship|Science citizenship]]
- [[Topics/Reading skills|Reading skills]]
- [[Topics/Rearranging formulae|Rearranging formulae]]
- [[Topics/Sampling|Sampling]]
- [[Topics/Science|Science]]
- [[Topics/Sequences|Sequences]]
- [[Topics/Shape|Shape]]
- [[Topics/Simultaneous Equations|Simultaneous Equations]]
- [[Topics/Standard Index Form|Standard Index Form]]
- [[Topics/Statistics|Statistics]]
- [[Topics/Symmetry|Symmetry]]
- [[Topics/Using ICT in Science Teaching|Using ICT in Science Teaching]]
- [[Topics/Using images|Using images]]
- [[Topics/Visualisation|Visualisation]]
You can browse our resources by topic here, or choose a subject / grade category here:
Relevant resources
| Algebra | What's Possible? | |

|
Many numbers can be expressed as the difference of two perfect squares. What do you notice about the numbers you CANNOT make? This lesson idea is about exploring and noticing structure(ta).
The collection of NRICH activities are designed to develop students capacity to work as a mathematician. Exploring, questioning, working systematically, visualising, conjecturing, explaining, generalising, justifying, proving are all at the heart of mathematical thinking. This particular resource has been adapted from an original NRICH resource. NRICH promotes the learning of mathematics through problem solving. NRICH provides engaging problems, linked to the curriculum, with support for teachers in the classroom. Working on these problems will introduce students to key mathematical process skills. They offer students an opportunity to learn by exploring, noticing structure and discussing their insights, which in turn can lead to conjecturing, explaining, generalising, convincing and proof. The Teachers’ Notes provided focus on the pedagogical implications of teaching a curriculum that aims to provoke mathematical thinking. They assume that teachers will aim to do for students only what they cannot yet do for themselves. As a teacher, consider how this particular lesson idea can provoke mathematical thinking. How can you support students' exploration? How can you support conjecturing, explaining, generalising, convincing and proof?. | |
| Area | Circles, frustums and cylinders revision | |

|
Measure the volumes of objects This resource offer students the opportunity to engage in active learning(ta) - measuring and calculating using large size cylinders and frustums. This lesson brings great opportunity for small group "dialogic teaching(ta)". Open-ended and closed questioning(ta) of students can be used to draw on their existing knowledge and extend their understanding. The teacher provides a practical commentary below.
| |
| Assessment | Changing KS3 Questions for Engaging Assessment | |

|
A large set of questions grouped by topic, paper, and national curriculum level Test questions are often seen as uninteresting and useful only to assess pupils summatively. This resource however allows questioning(ta) to be used to support pupils’ revision, creativity and higher order(ta) problem-solving in class. The tasks could be conducted via whole class(ta) discussion(ta) or assessment(ta), perhaps using mini-whiteboards(tool), or in small group work(ta) situations.
| |
| Astronomy | Recreating the Big Bang | |

|
An introduction to the creation of the Universe. This presentation offers a tour of the European Organization for Nuclear Research (CERN) and explains why it is worth spending money on one experiment. It then delves into particle physics, looking at sub-atomic particles to offer analogies for what these particles are. The session focuses on whole class(ta) dialogue(ta) and higher order(ta) thinking skills as well as exploring scientific language(ta). This 4th session and the 5th are together the most theoretically complex and they present challenges to young peoples world views. As such they are led as much by their questions(ta) as by the presentation.
| |
| Astronomy | Astronomy Master Class | |

|
An overview of of six astronomy-related lessons resources (SC019 to SC0024) The Astronomy Master Class was developed to inspire the next generation of scientists and in particular physicists. Although this course of 6 lessons is framed mostly around the science of astronomy, it draws on many themes from physics and aims to show how they all can link together. Additionally, it is structured so that it deliberately does not cut across material in most standard GCSE science courses and does not aim to answer every question. A deliberate part of the design was to visit each topic area only briefly and leave students hungry for more.
| |
| Astronomy | Celestial Wanderers | |

|
Why would we fly to another planet to study its rocks? Drawing on a rich range of sources, this presentation allows the teacher to introduce planetary geology(topic), something not normally studied until degree level. It uses the narrative(ta) of the Voyager Probes journey to illustrate the vastness of the solar system(topic) and also the challenges of designing a spacecraft to travel that far. It ends with a discussion of the history(topic) of Mars, and how the differences between it and the Earth resulted in Mars loosing its water and atmosphere whereas we have kept ours.
| |
| Astronomy | It's full of stars | |

|
Using a telescope and considering how those early astronomers may have worked Astronomy(topic) has been practiced for centuries and doesn't require expensive equipment! This first session aims to train the whole class(ta) to use a telescope and, hopefully, to provide an opportunity to engage in some active learning(ta). The lesson includes some naked-eye observations and describes how modern technology helps scientists know where to look. You can explore the scientific method(ta) and language(ta) at this point, using targeted questioning(ta)/differentiation(ta). Students may be able to engage in an inquiry(ta)-based project around this work, perhaps for homework(ta).
| |
| Astronomy | Alien Life | |

|
Are we alone? This last of six presentations to recruit students for A level physics, is more light-hearted and simpler than the two previous resources. It considers the arguments around whether or not humanity is alone and includes an initial look at the bizarre nature of many of the claims of alien encounters - including a fictional one for good measure - before moving onto the more serious side of alien hunting. It concludes with a probabilistic argument based on the Fermi paradox.
| |
| Astronomy | Stars in the sky: what's up? | |

|
Use a software planetarium and encourage students to think about astronomy This activity offers an opportunity for whole class(ta) discussion(ta) and questioning(ta) centred around the use of the Stellarium. It also affords good opportunities for self-directed study or homework(ta) extensions, including perhaps the use of free mobile apps(tool) (see below). There are also opportunities for some cross curricula(i) discussion of geography (navigation by stars) and history or literacy in relation to the ancient world.
| |
| Biodiversity | Using Science to Support Biodiversity | |

|
A virtual field trip to study biodiversity. This is an investigation(ta) in a virtual field trip to Dartmoor National Park. It involves research, designing a scientific investigation and analysing the results.
| |
| Blogs | Digital Reporters at Camp Cardboard | |

|
Children using iPads to blog about Cardboard Sculptures This activity is a cross curricula(subject) activity, involving a collaborative(tool) approach, giving children the opportunity to work together on a blog. Children were encouraged to engage in group talk(ta) and discussion(ta) in the classroom to reflect on the activity they were to report on. The activity furthers e-skills(topic) and e-safety(topic) through the use of whole class(ta) participation. The specific art activity provided a great stimulus for the blogging. Equally, however, this approach could be applied to any event in or out of school. The use of blogging and social media gave the opportunity for children to share their ideas with a wider audience, and also gave opportunities for real-time feedback to their work. The use of hand-held technology also enabled active learning(ta) as the portability of the iPads and iPods allowed them to be used outside the classroom.
| |
| Blogs | Creating and Using OER to Promote Best Practice | |

|
One school's approach to sharing and promoting best practice using a blog This lesson idea encourages collaboration(ta) between teachers in order to develop and share practice(i) across a school. Blogs provide excellent opportunities for children and adults to share ideas and work together. They encourage and enable dialogue(ta) between a writer - or group of writers - and an audience, allowing for quick and easy feedback. They enable questions(ta) to be asked and answered quickly. This example shows a blog being used to encourage discussion(ta) to enable curriculum planning(topic) and curriculum development(topic).
| |
| Consecutive Sums | Using Prime and Square Numbers - How Old Am I? | |

|
Last year I was square, but this year I am in my prime. How old am I? This short activity offers opportunity for pupils to engage in mathematical thinking(ta) and higher order(ta) problem solving/reasoning(ta). They should be able to make links between different areas of mathematics and explore their ideas in whole class(ta) discussion(ta) and questioning(ta).
| |
| Digital Art | Creating Digital Painting using iPads | |

|
Children using iPads to create observational drawings of flowers This activity is a cross-curricular(subject) activity, that gives children to opportunity to work independently on an art activity that also encourages the development of E-skills(topic). This activity encouraged inclusion(ta) as the children's final work was displayed as a collaborative(tool) piece, where all children had the opportunity to make an equal contribution.
In this instance, the children created observational drawings of flowers. However, the subject of the art could change to fit with any topic across the curriculum. The use of hand-held technology could also active learning(ta) as the portability of the iPads and iPods would allow them to be used outside the classroom, thus enabling observational drawings to be made in a range of locations. | |
| Discussion | Discussion in Science Teaching | |

|
Equip yourself to run a discussion in class This resource is aimed at developing student teachers’ skills in working with discussion(ta). It can be presented to them as a hand-out to accompany an activity or read as reference material. See it online at BEEP website. Although it uses a science context, the real focus of the resource is managing and organising discussion-based activities. It provides guidance on:
| |
| Ethics | Designer Babies | |

|
When does life actually begin? By using an informative web tutorial, this resource aims to stimulate discussion(ta) on the ethics(topic) of modern biology. A worksheet asks students where they stand and reassures them that their response might be kept private. You might also consider using a blog, chat room or other ICT tool to record the questioning(ta) and reasoning(ta) around this topic. A teaching section offers guidance on 'teaching argument' using 'Toulmin’s model of argument' and 'The IDEAS project'.
| |
| Ethics | Ethical issues in human reproduction | |

|
Why does reproduction raises so many ethical issues? When does life begin? This lesson outline stimulates A-level students to engage in discussion(ta), develop their reasoning(ta) skills and increase their awareness of the bioethical(topic) issues involved in human reproduction.
Background texts and open-ended questioning(ta) about human reproduction, contraception and IVF are provided as the stimulus. Small group discussion about these topics, writing on post-it notes, and reading case studies aim to get students reasoning(ta) to justify their opinions, and to compare and evaluate competing views. Finally, whole class(ta) discussion synthesises the emerging ideas and encourages students to consider changing their positions or adding additional issues to a recording table. | |
| Ethics | Cloning | |

|
Cloning - Potential and Issues The topic of the ethics(topic) of modern biology needs to draw on a wider range of sources than a printed book may provide. This resource uses a web tutorial interspersed with external links to news and comment. Rather than leave the students to explore too many interests, a worksheet with questions enables the teacher to focus the students on a subset of the material. You can adapt this to your particular need, for example, if you wanted students to have a discussion(ta)in small groups. You might also consider using a blog, chat room or other ICT tools to record the questioning(ta) and reasoning(ta) around this topic. The lesson-planning proforma (or draft lesson plan) includes a list of objectives that shows the scope of the material.
| |
| Force | What makes a good paper airplane? | |
|
| |
| Force | Force in the early years | |
|
Thinking about the language of force This lesson idea highlights the scientific language(ta) around the topic of force, and through group work(ta) and whole class(ta) dialogue(ta) engages pupils in inquiry(ta) and the scientific method(ta) surrounding force.
| |
| Force | Which material makes a good parachute? | |

|
A simple investigation into parachutes and air resistance This activity supports a number of learning types:
| |
| Force | What floats and what sinks | |

|
Is getting in the bath a way to lose weight? This activity supports a number of learning types:
| |
| Force | Building bridges from a piece of A4 paper | |

|
A bridge too far... This activity supports a number of learning types:
| |
| Genetics | How DNA is sequenced: the stages | |

|
The complexity and scale of genome sequencing Students match diagrams of the stages of DNA sequencing with a list of text descriptions of the process. The lesson can involve students discussing in pairs / group work(ta), followed by a teacher or student-led plenary. Students would share ideas, come to a consensus and check the ‘whole class(ta) response’ with their version. The teacher's questioning(ta) can focus on scientific method(ta) and use of scientific language(ta). The lesson idea provides opportunities for the effective use of assessment(ta).
| |
| Genetics | Human Genome Project: from Sequencing to Sharing Genomic Information | |

|
Discuss and share economic, political and ethical issues. This resource provides guidance on how to use whole class(ta) discussion(ta) and/or small group work(ta) to engage students with the science and the economic, political, ethical(topic), legal and social issues of a scientific project such as the HGP. Its focus is on the scientific method(ta); language(ta) and the nature of scientific inquiry(ta).
| |
| Graph | Variation of human characteristics - Visualising Class data | |
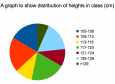
|
A big survey of ourselves, measuring hands, feet and more The lesson offers the opportunity to explore measurement, relationships between measurement, and ways to visualise and summarise this data. The use of ICT(i) allows the teacher to enter data and for pupils to immediately see the impact this has on the pie chart and frequency tables (which are automatically updated). This also allows the teacher to change the 'range' for the frequency counts, and discuss with pupils the impact of this on the pie chart, and whether this is a good representation - encouraging the use of mathematical language(ta) and scientific method(ta) throughout. In collecting the data pupils have opportunity for some self-directed group work(ta) - to measure various lengths as described below - and the teacher could use whole class(ta) questions(ta) to explore the strategies taken to conduct this investigation(ta).
| |
| Handling Data | Olympic Records | |

|
Can you deduce which Olympic athletics events are represented by the graphs? This lesson idea is about reasoning, justifying, convincing and proof(ta).
The collection of NRICH activities are designed to develop students capacity to work as a mathematician. Exploring, questioning, working systematically, visualising, conjecturing, explaining, generalising, justifying, proving are all at the heart of mathematical thinking. This particular resource has been adapted from an original NRICH resource. NRICH promotes the learning of mathematics through problem solving. NRICH provides engaging problems, linked to the curriculum, with support for teachers in the classroom. Working on these problems will introduce students to key mathematical process skills. They offer students an opportunity to learn by exploring, noticing structure and discussing their insights, which in turn can lead to conjecturing, explaining, generalising, convincing and proof. The Teachers’ Notes provided focus on the pedagogical implications of teaching a curriculum that aims to provoke mathematical thinking. They assume that teachers will aim to do for students only what they cannot yet do for themselves. As a teacher, consider how this particular lesson idea can provoke mathematical thinking. How can you support students' exploration? How can you support conjecturing, explaining, generalising, convincing and proof?. | |
| ICT | Creating Instructional Videos | |

|
Children create instructional videos to upload to YouTube This activity is a cross-curricular(subject) activity with a literacy focus, involving a collaborative(tool) approach, giving children to opportunity to work together to produce a set of instructional resources. Children were encouraged to engage in group talk(ta) and discussion(ta) in the classroom to reflect on what they should include in their videos. The activity furthers e-skills(topic) through the use of whole class(ta) participation. It develops e-safety(topic) skills through discussion of the issues relating to posting digital content online. Children were allowed to choose their own subject for the video, although this could be set by a teacher with a specific outcome in mind, or could be tailored to cover a particular topic or subject. It could, for instance, be used to explain their mathematical thinking(ta).
| |
| ICT | Data Logging inservice booklet | |

|
A compendium of CPD and ITE activities on why we use sensors and the practicalities of implementing their use Activities and advice for using ICT(i) for use in inquiry(i) based learning and the scientific method(i).
| |
| ICT | Primary Science Curriculum Activities with Sensors | |

|
A compendium of investigations with sensors in primary science This resource provides a set of activities to engage pupils in inquiry(ta) based learning in the scientific method(ta), often making effective use of ICT(i) and sensors(tool). The activities involve whole class(ta) questioning(ta) and collaborative(ta) group work(ta).
| |
| ICT | Infant and Primary Science Activities with Sensors | |

|
A compendium of investigations with sensors in primary science. This is a compendium of activities to engage pupils in inquiry(ta) based learning in the scientific method(ta), often making effective use of ICT(i) and sensors(tool). The activities involve whole class(ta) questioning(ta) and collaborative(ta) group work(ta).
| |
| ICT | IT in Secondary Science | |

|
A whole book of ideas for using generic ICT tools in science This book provides resources and lesson ideas with ICT(i) as a key focus for use in inquiry(ta) based learning and the scientific method(ta). It offers opportunities for use of group work(ta) and collaboration(ta) as well as whole class(ta) questioning(ta).
| |
| ICT | Data Logging and Control | |

|
A compendium with numerous ideas for using sensors to teach science. This book provides a set of resources and lesson ideas with ICT(i) as a key focus for use in inquiry(ta) based learning and the scientific method(ta). It offers opportunities for use of group work(ta) and collaboration(ta) as well as whole class(ta) questioning(ta).
| |
| ICT | IT in Primary Science | |

|
A whole book of ideas for using generic ICT tools in science This book is a compendium of lesson ideas with ICT(i) as a key focus for use in inquiry(ta) based learning and the scientific method(ta). It offers opportunities for use of group work(ta) and collaboration(ta) as well as whole class(ta) questioning(ta).
| |
| Investigation | Persuasive argument and evidence-based conclusions about the best car | |

|
Got a new motor? Talk about your investigation like a scientist This activity involving inquiry(ta)aims to develop children’s ability to support their conclusions with evidence. The teacher will model(ta) and encourage the use of the language(ta) that children require to discuss or present their data. The teacher can explain their rationale using the lesson below.
| |
| Investigation | Consecutive Sums | |

|
Can all numbers be made in this way? For example 9=2+3+4, 11=5+6, 12=3+4+5, 20=2+3+4+5+6 By definition, a problem is something that you do not immediately know how to solve, so learning how to solve something unfamiliar is not straightforward. Tackling an extended problem is difficult.
This lesson gives pupils an opportunity to engage in mathematical thinking(ta) and develop their higher order(ta) thinking skills on a problem that is accessible but which has interest. For example, the problem is presented in diagrammatic and numerical ways. The plan suggests several visualisation(ta) methods to present the same underlying task. It should be useful for teachers to compare these different presentations and either to select the one that they feel will be most useful for their pupils or explore ways for the pupils to see the links between the different methods. The assessment(ta) ideas, using other pupils' solutions from the NRICH website are widely applicable to other problems too. | |
| Learning objectives | Writing Learning Objectives in Primary Science | |

|
How are learning objectives supposed to work? How can one achieve mastery in writing learning objectives? This resource encourages teachers to think about ways to link learning objectives(ta) to the curriculum which also helps to conceptualise their teaching schemes. It also helps children to understand what they are learning and what they are aiming for. The resource brings together key ideas, looking at specific outcomes from activities, vocabulary(ta), differentiation(ta), resources and curriculum development(topic) and short term planning(ta). It could be used as a 'refresher' on ideas when planning lessons.
| |
| Literacy | Developing Language in Primary Science | |

|
Language development and the use of appropriate vocabulary(ta) is highlighted as important across the curriculum. Incorporating this consideration into science planning(ta) is important for meeting the target of developing language. The importance of language and talk in science – including through group work(ta), and Whole class(ta) dialogue – is highlighted elsewhere (and in the resource) but includes the ability to explain concepts, understand synthesising ideas (including those from other people and texts), and the need to read and write for different purposes, (including conceptual understanding, data presentation, etc). These are key ideas in communicating the scientific method(ta) | |
| Living things | Classifying and organising living things using images | |

|
Find different ways to classify living things This lesson offers opportunities to explore ways to classify living things as well as characteristics which might be relevant, and how to address difficulties that may arise when trying to classify things in this way. The activity may be enhanced by the use of ICT(i) software (e.g. Picasa) but could be carried out with paper-based resources.
This lesson presents a good opportunity for small group work(ta) and some inquiry(ta) into how we classify; and why some classification methods might be more useful, or more scientifically interesting than others. There is also a good opportunity to use different sorts of questioning(ta); to encourage pupils to question each other; to engage in peer assessment(ta) and to focus discussion(ta) on the scientific method(ta) using key vocabulary(ta). | |
| Materials | Heating and Cooling Materials | |

|
What happens when you heat and cool materials. In this inquiry(ta)-based lesson plan, students devise a ‘fair way’ to compare (mostly) physical changes in materials such as cheese and chocolate. They ask and answer questions about how to heat the materials and about using materials of the same size and shape. They also predict how substances may change and observe what actually happens.
The purpose of the lesson is to both support Year 2 students work on changing materials and to develop their ideas about ‘fair tests’. The activity thus offers an opportunity to assess(ta) how well students plan a test and observe change. | |
| Measuring | Measuring Light - Light and Dark | |

|
Light can be light, dark or somewhere in between This lesson involves the use of higher order questioning(ta) on scientific method(ta) topics to engage pupils in an inquiry(ta) relating to the nature of light, its measurement, and the use of sensors.
| |
| Measuring | Measuring Light - Does light shine through everything? | |
|
Using a sensor to see what's transparent and translucent This lesson involves the use of higher order questioning(ta) on scientific method(ta) topics to engage pupils in an inquiry(ta) relating to the nature of light, its measurement, and the use of sensors.
| |
| Measuring | Measuring Temperature - Cold and Hot | |
|
Put a number on the meaning of hot and cold This lesson involves the use of higher order questioning(ta) to engage pupils in an inquiry(ta) relating on how to record temperature and the use of sensors.
| |
| Measuring | Monitoring Temperature - Day and Night | |
|
What happens to the room's temperature when I'm not here? This lesson involves the use of higher order questioning(ta) on scientific method(ta) topics to engage pupils in an inquiry(ta) relating to recording temperature and the use of sensors.
| |
| Patterns | Exploring Pattern | |

|
Exploring patterns in mathematics Each chapter of this tutorial highlights the study skills(topic) required to work through the real world examples and activities given. There are problems to be solved, some of which involve higher order(ta) thinking skills (for example, being asked to correct a set of instructions), and all of which encourage the use of mathematical language(ta) and mathematical thinking(ta). The resource could also be used in class, or as a useful homework(ta) pack.
| |
| Polygons | Exploring properties of rectangles: Perimeter and area. | |

|
Do two rectangles that have the same area also have the same perimeter? A problem to inspire higher order(ta) questioning(ta) especially in whole class(ta) dialogic teaching(ta) encouraging pupils to engage in mathematical thinking(ta) and language(ta). You could use Geogebra(tool) in this investigation, as an example of same-task group work(ta).
| |
| Populations | Populations and ecosystems | |

|
Rabbits and vegetation - a real population case study Learning objectives are met using the following approaches:
| |
| Probability | Playing with Probability - Efron's Dice | |

|
I have some dice that are coloured green, yellow, red and purple... Efron's dice provide a discussion(ta) topic for joint reasoning(ta) - whole class(ta) or in group work(ta). Pupils can explore aspects of mathematical thinking(ta) particularly with relation to probability.
| |
| Progression | Developing Progression in Primary Science | |

|
Progression and the wonders of 'one-ness' and 'two-ness' A first part on ‘developing progression in science investigations’ could be used to prompt discussion on how far we expect pupils to develop, and the sorts of inquiry(ta) which encourage this.
The second part, 'indicators of Level 1 and 2ness', provides a useful set of criteria for assessing national curriculum levels. These criteria prompt thinking about assessment(ta) levels in curriculum development(topic). A concrete outcome of the activity may be to keep such criteria in a mark book for day-to-day use. | |
| QR codes | Editing Using QR Codes to Engage Children with Learning | |

|
Children using digital literacy to engage with reading and writing This lesson idea uses technology to promote active learning(ta) as resources were produced to be located and explored in a public park. The early stage of the activity, involving the creation of the resources by the children, required discussion(ta) involving the whole class(ta). Group talk(ta) was also employed as a strategy, with the children agreeing on a narrative(ta) outline relating to the event. The creation of the online materials encouraged development of e-skills(topic).
The later stages of activity, where the children were looking for clues, required them to ask questions(ta) and to take a collaborative(tool) approach to find a solution, based on the digital texts they found. | |
